Ceros, Polos, Frecuencia natural y Amortiguamiento
Un sistema, por ejemplo
![]()
se muestra como una descomposición de ceros y polos.
Las raíces del sistema pueden ser de dos tipos: ceros o polos.
Cero es todo valor de s que anule al numerador y por lo tanto a la función de transferencia.
Polo es todo valor de s que anule al denominador quedando la función de transferencia indefinida.
![]()
En el ejemplo resultaría que al igualar el numerador a cero obtenemos los ceros s=-1, s=-5
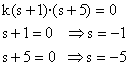
Al hacer el denominador cero se obtienen los polos s=0, s=-2, s=-0.5
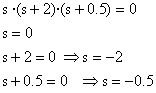
En cuanto a la representación de Bode, cada polo y cada cero da su propia contribución a la ganancia y a la fase de la función de transferencia.
Hay casos en que al descomponer la función de transferencia se encuentran raíces imaginarias. En este caso se suele trabajar con la frecuencia natural y el factor de amortiguamiento.
La frecuencia natural wn (sin amortiguar) es la frecuencia a que el sistema oscila cuando el factor de amortiguamiento es cero. En la representación de Bode, la frecuencia natural es el punto donde contribuye esta expresión.
El factor de amortiguamiento z es el factor que indica la oscilación que tendrá la respuesta de un sistema una vez excitado.
En estas dos gráficas siguientes se observa cómo varía la curva de ganancia real, y la curva de fase real, según el factor de amortiguamiento en una ecuación de segundo grado.
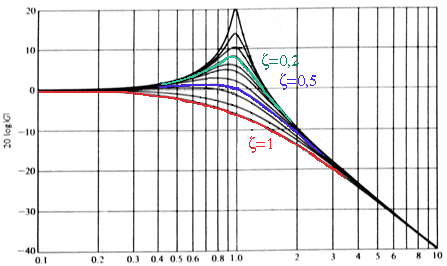

Una ecuación de segundo grado se define así:
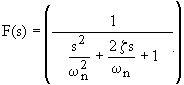
Sólo normalizando e identificando valores se pueden descubrir el factor de amortiguamiento(z) y la frecuencia natural (wn).
A partir del factor de amortiguamiento se puede tener una idea de la situación de los polos, ya que:
|
Factor de amort. |
Situación de polos |
Estabilidad |
|
z<-1 |
En el eje real positivo |
INESTABLE |
|
z = -1 |
Iguales en eje real positivo |
INESTABLE |
|
-1< z <0 |
Complejos en parte derecha |
INESTABLE |
|
z =0 |
Complejos en el eje imaginario |
ESTABLE |
|
0< z <1 |
Complejos en parte izquierda |
ESTABLE |
|
z =1 |
Iguales en el eje real negativo |
ESTABLE |
|
z >1 |
En el eje real negativo |
INESTABLE |
Con colores se distinguen las diferentes localizaciones de los polos, coincidiendo con el color del factor de amortiguamiento que se quiera.
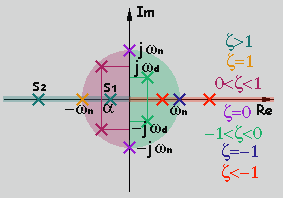
La condición de estabilidad es la siguiente: si existe algún polo en el semiplano derecho del plano, el sistema será inestable.
Esto se ve claro a partir del siguiente gráfico:
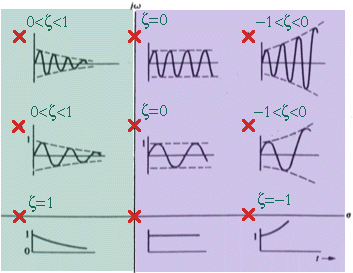
Explicación del criterio
En este gráfico se observa que si un polo se sitúa a la izquierda del plano, su señal de salida irá disminuyendo su amplitud siguiendo la forma de la envolvente exponencial que la limita.
En el caso que el polo esté situado en el eje imaginario la amplitud de la señal de salida se mantendrá constante, pero es lo que se llama una estabilidad asintótica, que quiere decir que con una ligera perturbación el sistema se puede convertir en inestable.
Si el polo está situado en el semiplano derecho, la amplitud de salida irá gobernada por una envolvente exponencial creciente, que lleva inequívocamente al sistema a un estado inestable.
Cuando el polo se sitúa en el eje real, la señal no oscila, pero sigue las mismas normas que los casos anteriores.
Por tanto, en el gráfico estamos viendo cómo influye la situación de los polos en relación con la señal en el tiempo. Así, por muchos polos o ceros que haya en el semiplano izquierdo, a medida que el tiempo avanza van extinguiéndose, y sólo con que haya un polo a la derecha ganará dominará sobre los otros, y la inestabilidad se apoderará del sistema.