Ganancia y Fase

La ganancia es la relación entre la amplitud de la señal de salida y la amplitud de la señal de entrada, es decir, es aquello que modifica a la señal de entrada para que resulte una señal de salida.

La fase es la relación entre el ángulo de la señal de salida y el ángulo de la señal de entrada. Según los componentes de que esté formado el sistema, el ángulo de salida estará adelantado o retrasado respecto a la señal de entrada.

La ganancia y la fase de un sistema generalmente dependen de la frecuencia, a no ser que sus componentes no dependan de la frecuencia o estén dispuestos de manera que no influya. Para representar estas variaciones de ganancia y fase debido a la frecuencia se utilizan:

· Diagramas de Bode

· Trazados polares de Nyquist

· Carta de Nichols

Las bases teóricas para calcular la ganancia y la fase es la siguiente:

Una función de respuesta de frecuencia de lazo abierto en forma polar se representa como un módulo (ganancia) y un argumento (fase).

En forma de parte imaginaria y parte real se puede expresar como:

La ganancia se encuentra como la raíz cuadrada de la parte real al cuadrado más la parte imaginaria al cuadrado.

Y la fase como el arcotangente de la parte imaginaria entre la parte real.

donde la expresión puede ser un polo, un cero, un numerador entero, un denominador entero o la función de transferencia entera, siempre que Re sea la parte real de esta expresión e Im sea la parte imaginaria de la expresión.

La ganancia de una función con ceros y polos se puede calcular directamente, o calculando las ganancias particulares de cada raíz y multiplicando las ganancias de los ceros y dividiendo las ganancias de los polos.

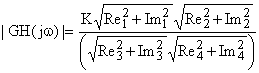
Pero trabajando con logaritmos la ganancia es la suma de los logaritmos de ganancia de los ceros menos los logaritmos de ganancia de los polos.

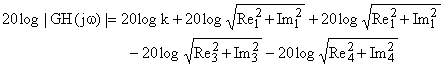
La fase de una función con ceros y polos se puede calcular directamente, o calculando las fases particulares de cada raíz y sumando las fases de los ceros y restando las fases de los polos.

También se puede escribir GH(jw) en la forma de Bode, descomponiendo la ganancia y la fase en sus polos y ceros.

Ejemplo:

Imaginemos que queremos ir buscando los valores de ganancia y fase de la función de transferencia:

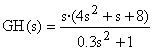
Si quisiéramos calcular a mano los valores, primero deberíamos pasar la función en función de s a función de w. La equivalencia es s=jw

Sustituiríamos y resultaría:

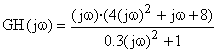
Y ahora se debería separar la parte real de la parte imaginaria. Para ello hay que operar, y tener en cuenta que j²= -1. Y separar la parte con j, de la parte libre de j.

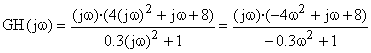
Ahora sería momento de encontrar las fórmulas generales de ganancia y de fase para esta función:

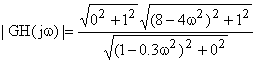
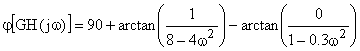
Una vez hechos estos pasos se deben ir dando valores a w, e ir calculando la ganancia y la fase. Después se hace el logaritmo en base 10 de la ganancia y se multiplica por 20.

|GH(jw)|dB = 20 log |GH(jw)|

Ya se puede ir completando la tabla:

Frecuencia w	Ganancia	Ganancia en dB	Fase en grados
0.1	0.80	-1.96	90.71
1	5.89	15.4	104.03
5	70.79	37	86.88
150	1999.86	66.02	89.9

Con el programa del banco de pruebas sólo se tienen que insertar los coeficientes y la frecuencia a la que se quieren los cálculos.