Zeros, Pols, Freqüència natural i Esmorteïment
Un sistema, por exemple
![]()
es mostra com una descomposició de zeros i pols.
Les arrels del sistema poden ser de dos tipus: zeros o pols.
Zero és tot valor de s que anul·li el numerador i per tant, la función de transferència.
Pol és tot valor de s que anul·li el denominador quedant la funció de transferència indefinida.
![]()
En el exemple resultaria que en igualar el numerador a zero obtenim els zeros s=-1, s=-5
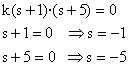
En fer el denominador zero s'obtenen els pols s=0, s=-2, s=-0.5
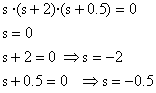
Respecte a la representació de Bode, cada pol i cada zero dóna la seva pròpia contribució al guany i a la fase de la funció de transferència.
Hi ha casos en què en descomposar la funció de transferència es troben arrels imaginàries. En aquest cas s'acostuma a treballar amb la freqüència natural i el factor de esmorteïment.
La freqüència natural wn (sense esmorteir) és la freqüència a què el sistema oscil·la quan el factor d'esmorteïment és zero. En la representació de Bode, la freqüència natural és el punt on contribueix aquesta expressió.
El factor de esmorteïment z és el factor que indica l'oscil·lació que tindrà la resposta d'un sistema una vegada excitat.
En aquestes dues gràfiques següents s'observa com varia la corba de guany real, i la corba de fase real, segons el factor d'esmorteïment en una equació de segon grau.
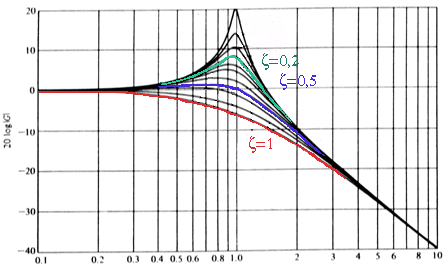
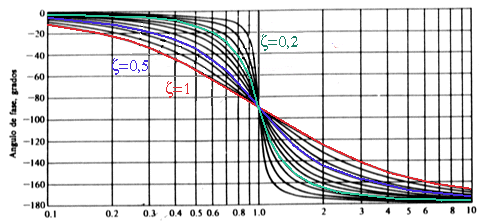
Una equació de segon grau es defineix com:
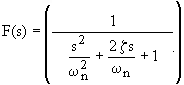
Només normalitzant i identificant valors es poden descubrir el factor d'esmorteïment(z) i la freqüència natural (wn).
A partir del factor d'esmorteïment es pot tenir una idea de la situació dels pols, ja que:
|
Factor d'esmort.. |
Situació de pols |
Estabilitat |
|
z<-1 |
A l'eix real positiu |
INESTABLE |
|
z = -1 |
Iguals, a l'eix real positiu |
INESTABLE |
|
-1< z <0 |
Complexes a part dreta |
INESTABLE |
|
z =0 |
Complexes a l'eix imaginari |
ESTABLE |
|
0< z <1 |
Complexes a part esquerra |
ESTABLE |
|
z =1 |
Iguals, a l'eix real negatiu |
ESTABLE |
|
z >1 |
A l'eix real negatiu |
INESTABLE |
Amb colors es distingeixen les diferents localitzacions dels pols, coincidint amb el color del factor d'esmorteïment que es vulgui.
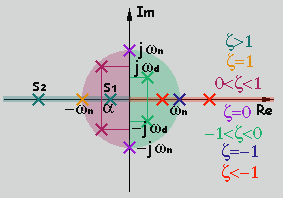
La condició d'estabilitat és la següent: si existeix algun pol en el semiplà dret del pla, el sistema serà inestable.
Això es veu clarament a partir del següent gràfic:
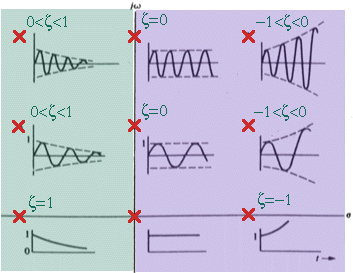
Explicació del criteri
En aquest gràfic s'observa que si un pol es sitúa a l'esquerra del pla, el seu senyal de sortida anirà disminuint la seva amplitud seguint la forma de l'envolvent exponencial que la limita.
En el cas que el pol estigui situat a l'eix imaginari, l'amplitud del senyal de sortida es mantindrà constant, però és una estabilitat assimptòtica, que vol dir que amb una lleugera perturbació el sistema se pot convertir en inestable.
Si el pol està situat en el semiplà dret, l'amplitud de sortida anirà governada per una envolvent exponencial creixent, que porta inequívocament al sistema a un estat inestable.
Quan el pol es sitúa a l'eix real, el senyal no oscil·la, però segueix les mateixes normes que els casos anteriors.
Per tant, en el gràfic estem veient com influeix la situació dels pols en relació amb el senyal en el temps. Així, per molts pols o zeros que hi hagi en el semiplà esquerra, a mida que el temps avança van extinguint-se, i només que hi hagi un pol a la dreta dominarà sobre els altres, i la inestabilitat s'apoderarà del sistema.