Laplace

Les funcions de transferència amb què es treballa en el curs estan en funció de s. Què significa “s”? s és la variable complexa de la freqüència.

Però en la vida real es treballa amb funcions de variable real (generalment temps o distància). La transformada de Laplace reemplaça aquestes variables reals (temps) per variables complexes (freqüència). En el domini del temps les expressions acostumen a ser complicades, amb exponents i integrals, que són molt enutjoses de manejar. Llavors la transformada de Laplace converteix aquestes funcions en funció del temps (t) a funcions en funció de la freqüència (s). Les expressions resultants són molt més senzilles d'utilizar. La tècnica de transformada de Laplace estalvia càlculs i dóna una visió molt més clara dels conceptes.

Laplace també resulta molt útil a l'hora de formar les funcions de transferència, ja que relaciona el sistema físic elèctric amb una expressió matemàtica.

Per donar un exemple de com es transforma un circuit elèctric a una funció de transferència en funció de s només s'han de conéixer algunes equivalències:

Un condensador es representa com 1/Cs, una bobina es representa amb Ls i una resistència, com no varia amb la freqüència queda constant R.

La forma d'anar formant la impedància total del sistema és exactament la mateixa com si tots els components fossin resistències, però prenent els seus equivalents en s.

Així, dos elements en sèrie es suman: Z=Z1+Z2

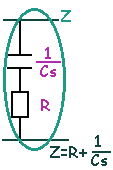
I dos elements en paral·lel segueixen la forma:

I d'aquesta manera es van construint les funcions de transferència.

Als sistemes funcionals les lletres majúscules s'utilitzen en l'entrada i sortida dels sistemes i les funcions de transferència representen transformades de Laplace de quantitats que són funcions de la variable complexa s. Les funcions de s generalment s'abreugen amb una lletra majúscula que apareix sola. Les funcions de freqüència mai s'abreugen.

Com a definició de Laplace s'acostuma a donar:

“Sigui f(t) una funció real d'una variable real t definida per t>0. Llavors,

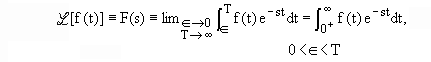
és el que s'anomena la transformada de Laplace de f(t).”

s és una variable complexa definida per

on  és la part real d'una variable complexa s, i s'acostuma a escriure como Re(s) i w també és una variable que en anar acompanyada per j és la part imaginària de s: Im(s).

S'ha inclòs una taula d'antitransformades, és a dir per passar del domini de la variable complexa (s) a la variable real (t). Així es podran donar els resultats en funció del temps.